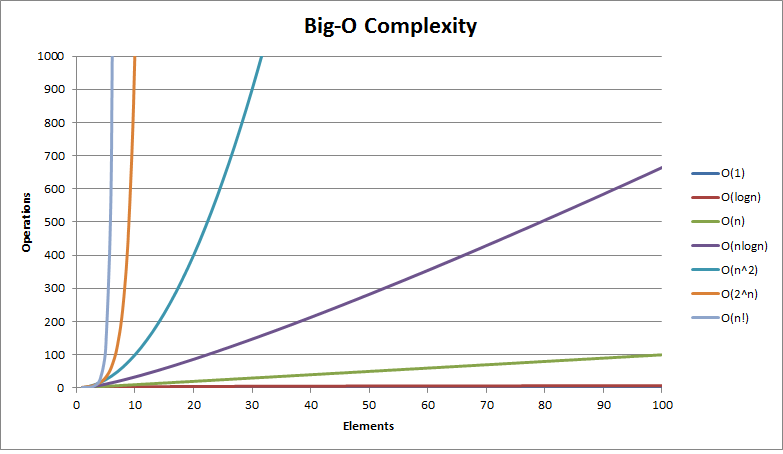
-compliments of http://bigocheatsheet.com/

Introduction

In our previous intro to asymptotic notation post, we talked about Big-O notation. Today, we're going to expand upon that by showcasing common Big-O runtimes and how to identify what that runtime looks like in code. We'll be using javascript for the code itself.

N

for(var n = 1; n <= 5; n++){
  console.log(n);
}

The function above prints out every number between 1 and 5. Since the function will print out each number, one at a time, until it reaches the end, it has a best and worst case (Big Theta Θ) Θ(N). It'll progress linearly in runtime as the value of N goes up.

log(N)

Now let's talk about log(N) runtimes. I've made a function called binaryChop that takes a sorted list of numbers (array) and a number we want to find (findNum)

var binaryChop = function(findNum, array){
  console.log("The array we're searching is...", array);
  // looks to see if number exists within sorted array
  if (findNum > array[array.length - 1] || findNum < array[0] ){
    return console.log("Can't find number!");
  }
  // sets target to check against to middle of array
  var halfLength = Math.floor(array.length/2);
  var target = array[halfLength];   
  console.log("target is ", target);

  // if target is equal to findNum, found!
  if (target === findNum){
    return console.log("Found!");
  // recursively call binaryChop again with shortened array
  } else if ( findNum < target ){
    var slicedArray = array.slice(0, halfLength)
    binaryChop(findNum, slicedArray);
  } else if ( findNum > target ){
    var slicedArray = array.slice(halfLength, array.length)
    binaryChop(findNum, slicedArray);
  } else {
    return console.log("Can't find number!");
  }
}

var secretNum = 3
var numbers = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19];
binaryChop(secretNum, numbers);

If the number doesn't exist, it'll print out that the number wasn't found, if the number does exist, it'll find it by recusively calling itself and chopping the original array in half each call.

We take the 1st half of the array if the number we're looking for is less than the number at the halfway point (in the above example 10), else, we take the 2nd half.

Here's an example of this function being ran with the code above.

Best Case (Big-Ω)

There's a few best cases (Big-Omega). First is if the number doesn't exist in the array, it'll just return Can't find number!. The other best case is if the target ends up being the number we're looking for. Therefor best case is a constant of 1 or Ω(1). This isn't very helpful, so we'll stick with worst cases.

Worst Case (Big-O)

Since the function is called with half the numbers being cut out each time, the worst case scenario is log(N). The worst case for the above function would occur if the secretNum was within the 1st position or last position of the numbers array (so 1 or 19).

For completeness, I tested the above function, and it recursively called itself 4 more times before it could find 1, so if 5 is the worst case for a group of 19 numbers, that's still less than 19, which would be the worst case for a linear search where 19 was the number (so O(log(N)) is better than O(N) in most cases).

N²

for(var i = 1; i <= 5; i++){
  for(var n = 1; n <= 5; n++){
    console.log(n);
  }
}

Big-O log(N²) can happen when you have a loop iterating within a loop that's iterating.

In the above example, we go through 5 iterations of counting to 5, so it counts to 5 5 times. Since 5² = 25, we can see that this runtime can take off if it's input values get too big.

Conclusion

I hope this showcases some good examples of common Big-O runtimes. I look forward to expanding upon this with you all in the future.

Thanks for reading and please feel free to comment below if you have any questions.